记一个关于 RMSNorm 实现上的细节

背景

在 RMSNorm 的实现中，都会强制把输入转为 float32 再进行计算，主要为了避免在计算过程中出现溢出的情况，特别是 float16。

bfloat16 由于动态范围更大，通常不会出现溢出问题，但在一些特定的计算场景下，仍然可能会遇到精度问题。因此，在实现 RMSNorm 时，强制转换为 float32 是一个通用的做法。

RMSNorm

import torch
import torch.nn as nn

class RMSNorm(nn.Module):
    def __init__(self, dim, eps=1e-8):
        super(RMSNorm, self).__init__()
        self.weight = nn.Parameter(torch.ones(dim))
        self.eps = eps

    def forward(self, x):
        # 强制转换为 float32
        x = x.to(torch.float32)
        # 计算 RMS
        rms = torch.sqrt(x.pow(2).mean(dim=-1, keepdim=True) + self.eps)
        return self.weight * x / rms

如果不转为 float32，精度情况

如果不将输入转换为 float32，直接使用 float16 进行计算，可能会导致数值精度的问题。例如，在计算 RMS 时，由于 float16 的表示范围和精度有限，可能会出现梯度消失或爆炸的情况，从而影响模型的训练效果。如下图，

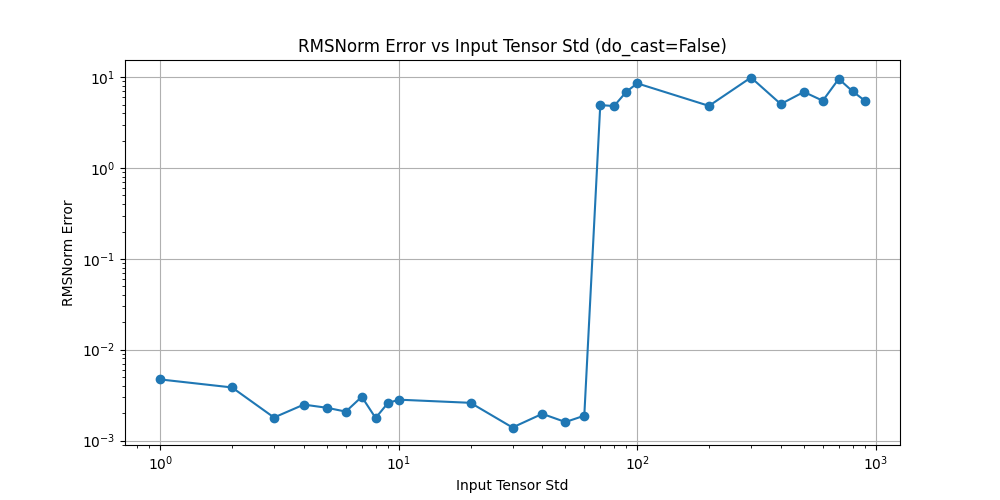
可以看到，std 在达到 70 之后，f32 和 f16 计算的误差马上就从 0.001 上升到 8.0，此时发生了 f16 的溢出，导致 RMSNorm 的输出变为 Infinity。

由于 float16 的表示范围有限，最大值只有 65504，很容易溢出。在 RMSNorm 中溢出的场景有两个：

1. 求和溢出：当输入的数据过大时，求和的结果可能超过这个范围，导致溢出为 Infinity
2. 平方溢出：在计算平方时，如果输入的数值过大，平方后的结果也会超过 float16 的表示范围，导致溢出为 Infinity

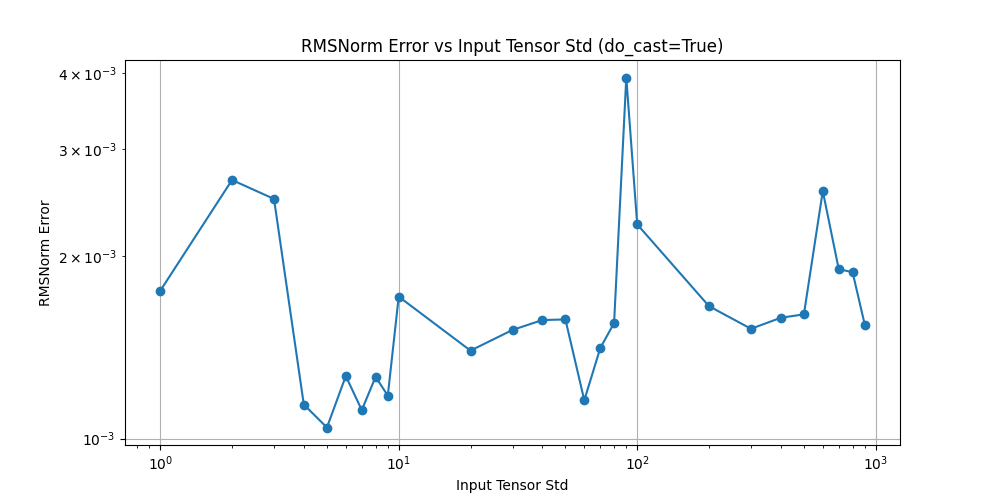
如果转为 float32，精度情况

如果将输入转换为 float32，计算过程中的数值精度问题会得到有效缓解。如下图所示，最大误差不超过 4e-3。

PyTorch 中的 LayerNorm 实现

PyTorch 官方提供了 LayerNorm 算子，可以直接调用。为了避免产生 f16 的溢出问题，PyTorch 在实现中将输入 data-type 和累积 data-type 分离。具体来说，输入数据仍然是 float16，但在计算过程中会转换为 float32 进行处理，最后再转换回 float16。

vectorized_layer_norm_kernel_impl 实现如下。可以看到，输入数据 X 是 float16 类型，但是累加结果时使用的是 T_ACC（通常是 float32），最后拷贝到输出 Y 时会进行隐式类型转换。

template <typename T, typename T_ACC,
typename std::enable_if_t<!std::is_same_v<T, double>, int> = 0>
__device__ __inline__ void vectorized_layer_norm_kernel_impl(
  const int N,
  T_ACC eps,
  const  T* __restrict__ X,
  const  T* gamma,
  const  T* beta,
  T_ACC* mean,
  T_ACC* rstd,
  T* Y){
    extern __shared__ float s_data[]; //if we made smem WelfordDataLN type, there would be bank conflicts,
    //as one thread would have to write 3 consecutive floats
    auto i1 = blockIdx.x;
    const T * block_row = X + i1 * N;
    WelfordDataLN wd = compute_stats(block_row, N, s_data);

    using vec_t = aligned_vector<T, vec_size>;
    const vec_t * X_vec = reinterpret_cast<const vec_t*>(block_row);
    const vec_t * gamma_vec = (gamma != nullptr) ? reinterpret_cast<const vec_t*>(gamma) : nullptr;
    const vec_t * beta_vec = (beta != nullptr) ? reinterpret_cast<const vec_t*>(beta) : nullptr;
    vec_t * Y_vec = reinterpret_cast<vec_t*>(Y + i1 * N);

    const int numx = blockDim.x * blockDim.y;
    const int thrx = threadIdx.x + threadIdx.y * blockDim.x;
    const int n_vec_to_read = N/vec_size;

    T_ACC rstd_val = c10::cuda::compat::rsqrt(wd.sigma2 + eps);

    // No tail, N is guaranteed to be multiple of vec size
    for (int i = thrx; i < n_vec_to_read; i += numx) {
      vec_t data = X_vec[i];
      vec_t out;

      // Computation is performed in T_ACC, X is cast to T_ACC and result is implicitly cast to T

      // NOTE: 为了简洁，我忽略了 gamma 和 beta 的 nullptr 检查
      #pragma unroll
      for (int ii=0; ii < vec_size; ii++){
        out.val[ii] = static_cast<T_ACC>(gamma_vec[i].val[ii]) * (rstd_val * (static_cast<T_ACC>(data.val[ii]) - wd.mean))
        + static_cast<T_ACC>(beta_vec[i].val[ii]);
      }

      Y_vec[i] = out;
    }
    if (thrx == 0) {
      mean[i1] = wd.mean;
      rstd[i1] = rstd_val;
    }
}